题目
题目描述
佳佳碰到了一个难题,请你来帮忙解决。
对于不定方程a1+a2+…+ak-1+ak=g(x),其中k≥2且k∈N,x是正整数,g(x)=x^x mod 1000(即x^x除以1000的余数),x,k是给定的数。我们要求的是这个不定方程的正整数解组数。
举例来说,当k=3,x=2时,分别为(a1,a2,a3)=(2,1,1)'(1,2,1),(1,1,2)。
输入格式
输入文件equation.in有且只有一行,为用空格隔开的两个正整数,依次为k,x。
输出格式
输出文件equation.out有且只有一行,为方程的正整数解组数。
输入样例
|
1 2 |
3 2 |
输出样例
|
1 2 |
3 |
说明
对于40%的数据,ans≤10^16;对于100%的数据,k≤100,x≤2^31-1,k≤g(x)。
题解
首先呢,\(g(x)\)我们是可以求解的,我们设\(n=g(x)\)
我们可以先写出\(n\)个1,我们发现它们之间有\(n-1\)个空隙,而我们的任务是寻找k个数,使k个数的和等于\(n\),于是我们就可以将问题转化成在\(n-1\)个空隙中选出\(k-1\)个空隙放挡板,形成的\(k\)个数的和正好就是\(n\)。
换句话说,我们要求\(C_{n-1}^{k-1}\)
对于样例的画图辅助理解
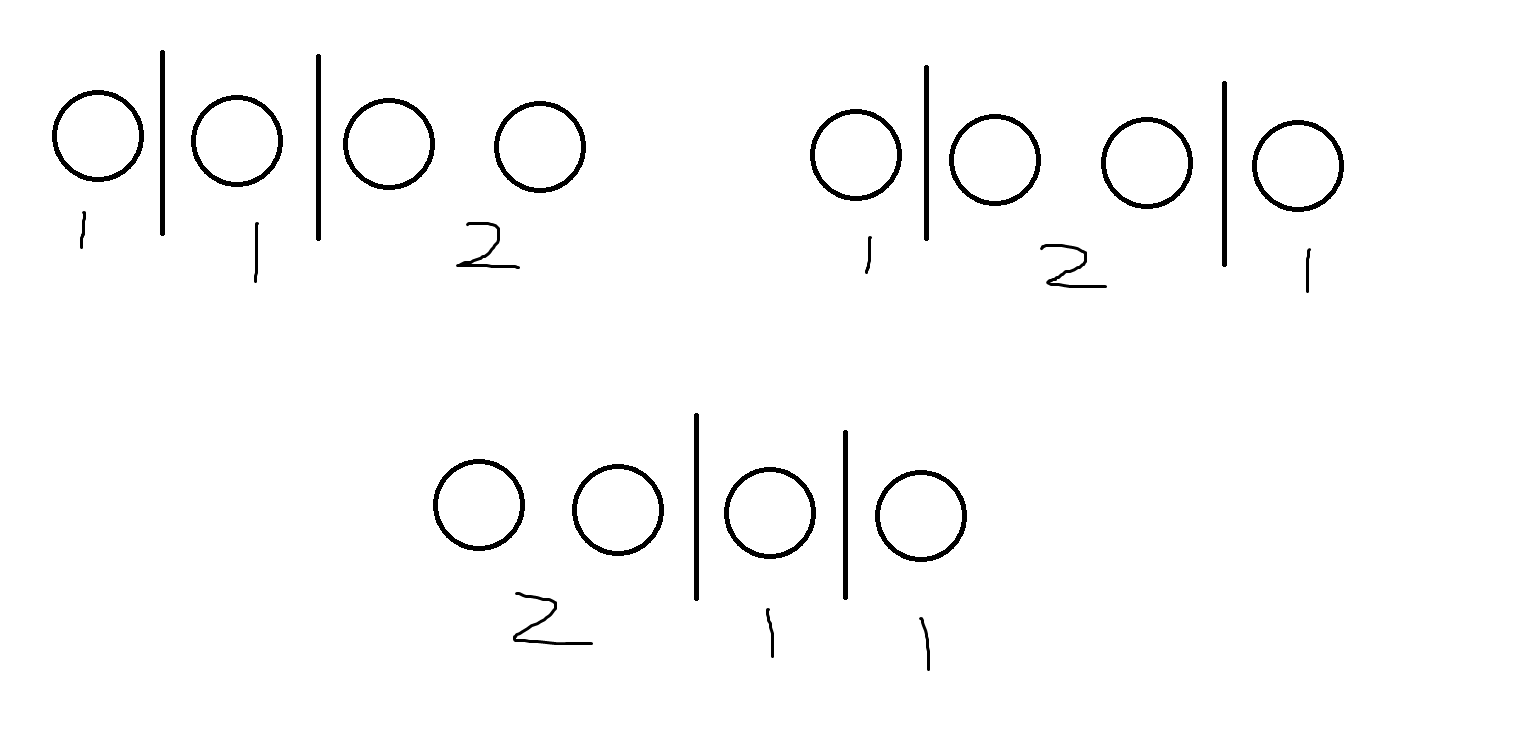
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
#include<iostream> #include<cstdio> using namespace std; typedef long long ll; const int MAXN = 100, mod = 1000, inf = 1000000; ll k, x, n; ll sum[MAXN], cnt = 1; ll qpow(ll a, ll b) { ll ans = 1; while (b) { if (b & 1)ans = ans * a%mod; a = a * a%mod; b >>= 1; } return ans; } void c(ll n, ll m) { sum[1] = 1, cnt = 1; for (int i = m; i >= m - n + 1; i--) {//对组合数公式进行了化简 for (int j = 1; j<MAXN; j++) { sum[j] *= i; } for (int j = 1; j<MAXN; j++) { if (sum[j] >= inf) { sum[j + 1] += sum[j] / inf; sum[j] %= inf; } } } for (int i = 2; i <= n; i++) { for (int j = MAXN-1; j >= 1; j--) { if (sum[j] == 0) continue; if (sum[j] >= i) { sum[j - 1] += sum[j] % i*inf; sum[j] /= i; } else sum[j - 1] += sum[j] * inf, sum[j] = 0; } } } int main() { ll k, x; cin >> k >> x; n = qpow(x, x); if (k - 1 <= 0 || n - 1 <= 0) { printf("0"); return 0; } c(k - 1, n - 1);//总共有n-1个间隙,要插k-1个隔板; int id; for (int i = MAXN - 1; i >= 1; i--) { if (sum[i]) { id = i; break; } } printf("%lld", sum[id]); for (int i = id-1; i >= 1; i--) { printf("%06lld", sum[i]); } return 0; } |