题目
描述
桌面上放了N个平行于坐标轴的矩形,这N个矩形可能有互相覆盖的部分,求它们组成的图形的面积。
格式
输入格式
输入第一行为一个数N(1≤N≤100),表示矩形的数量。下面N行,每行四个整数,分别表示每个矩形的左下角和右上角的坐标,坐标范围为–10^8到10^8之间的整数。
输出格式
输出只有一行,一个整数,表示图形的面积。
样例1
样例输入1
|
1 2 3 4 5 |
3 1 1 4 3 2 -1 3 2 4 0 5 2 |
样例输出1
|
1 2 |
10 |
题解
这里有篇很好的文章,对于深入理解有帮助
对于这道题目,第一想法就是用bool数组标记,最后统和,但是奈何数据范围不允许。
可以用扫描线+线段树维护,但是总觉得有点大动干戈。
而“离散化”这一奇妙的思想能帮我们优雅地解决这道题(然而样例不能很好体现)
我们首先来看看样例
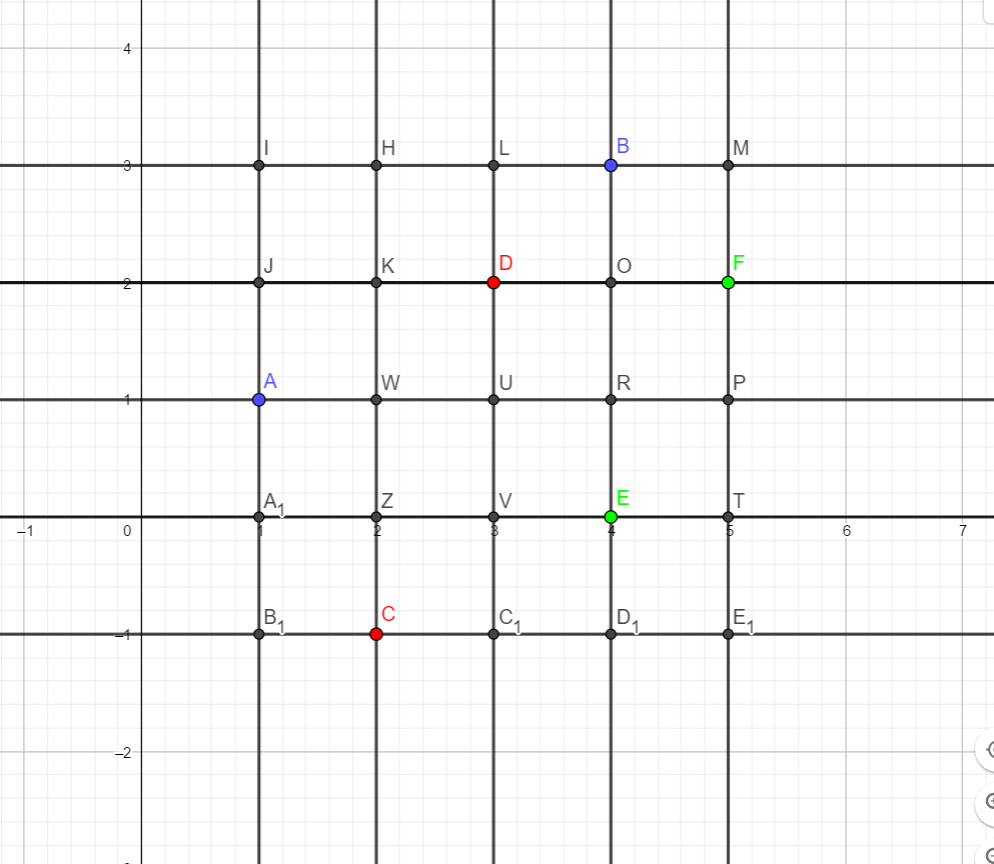
其中一样的颜色的点为一对输入(一个矩形),我们取出它们的横纵坐标,去重,排序,然后再去枚举,就得到了那些黑色的点。(有些和有颜色的点重复了)
其实到了这一步我们已经离散化了(还没明白?别急,先往下看)
于是我们枚举每一个黑色的点,让它和它右上方的黑点构成一个矩形,如果这个矩形在任意输入矩形内部,则对答案有贡献
这样子我们就做到了不重不漏(黑点枚举出来的矩形不重复,并且黑点构成的全部矩形肯定把输入矩形囊括在内)

到这里貌似就结束了,但是这种方法看上去还是在数格子?
让我们把输入改成
|
1 2 3 4 5 |
3 1 1 4 4 2 -1 3 3 4 0 5 3 |
再看看图像

我们的枚举量并没有随着坐标范围变大而变大,并且还是做到了不重不漏,其原因就是我们在枚举黑点的时候,本来是2的距离,转化成了该点与上个点相差2,而空间上这两个点还是相邻的,这就是离散化。
上面已经解释得很清楚了,代码就不写注释了。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; const int MAXN=203; long long x[MAXN],y[MAXN],x1[MAXN],x2[MAXN],y1[MAXN],y2[MAXN]; long long S,ans; int n; int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%lld%lld%lld%lld",&x1[i],&y1[i],&x2[i],&y2[i]); x[2*i-1]=x1[i]; y[2*i-1]=y1[i]; x[2*i]=x2[i]; y[2*i]=y2[i]; } sort(x+1,x+2*n+1); sort(y+1,y+2*n+1);//这里忘了去重,如果有重复的,(x[i+1]-x[i])*(y[j+1]-y[j])必定有一项为0,对答案没贡献 for(int i=1;i<=2*n-1;i++){ for(int j=1;j<=2*n-1;j++){ S=(x[i+1]-x[i])*(y[j+1]-y[j]); for(int k=1;k<=n;k++){ if(x[i]>=x1[k]&&y[j]>=y1[k]&&x[i+1]<=x2[k]&&y[j+1]<=y2[k]){ ans+=S; break; } } } } cout<<ans; return 0; } |
[latex]e=mc^2[/latex]
[mathjax]E=mc^2[/mathjax]
支持markdown