zkw大佬的PPT——统计的力量
虽然说这里有一些错误,但是zkw神犇讲的东西还是挺让人震撼的。
操作一:区间查询,单点修改
练习例题 CodeVS1080
这大概是zkw线段树最简单的操作了
如果你看过PPT的话,会发现我们对树的结点的访问是根据结点的二进制数来实现的:
子结点是父结点右移1位得到的,其中右子结点+1
所以说,叶子结点的最左边的那个结点无疑是很关键的,只要知道了它,我们访问其他叶子结点只要在它的id上加(i-1)就是第i个叶子结点。
建树
zkw线段树建树就是基于这样一种思想,由下到上:
|
1 2 3 4 5 6 7 8 9 10 11 |
inline void update(const int &p){ d[p]=d[p<<1]+d[p<<1|1]; } inline void build(){ for(p=1;p<=n+1;p<<=1);//范围坚持zkw的“多开就好” M=p;//记录下来 for(int i=p+1;i<=p+n;i++)read(d[i]);//更新叶子结点 for(int i=p-1;i;--i)update(i);//更新父结点 } |
单点修改
在此基础上,单点修改也很好执行:
|
1 2 3 4 5 6 |
inline void change(int x,int y){ for(d[x+=M]+=y,x>>=1;x;x>>=1){ update(x); } } |
区间查询
区间查询有点意思,
我们先来看一组数据。
如果你足够细心的话,应该能发现上面的操作有点问题,因为我们实际建出来的树并不是你想象的那样,而是下面这样:
对于
|
1 2 |
1 2 3 4 |
我们查询
|
1 2 |
2 3 |
的话
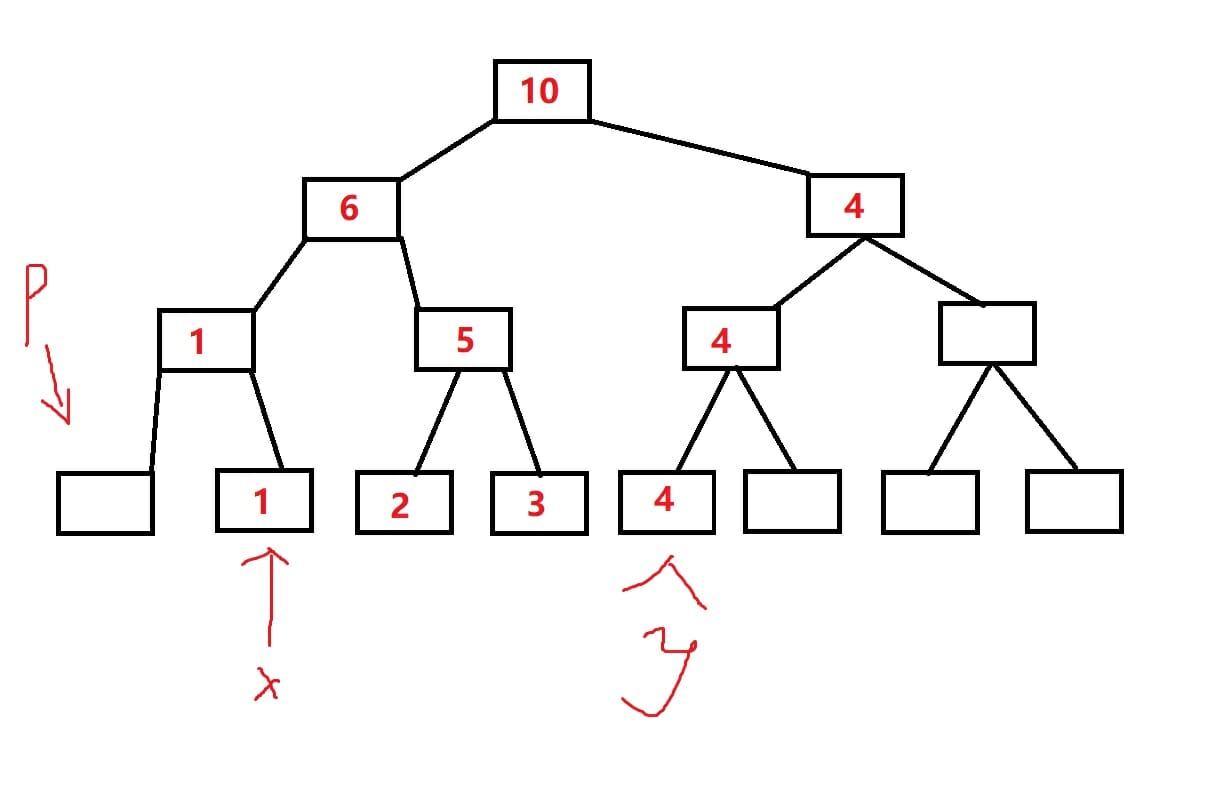
树就是这样的,我们把查询范围变成了一个开区间,然后让它们往上走,如果x是左子树,贡献右子树答案,如果y是右子树,贡献左子树答案。
直到它们有同一个父亲为止。
由于左子树和右子树只有最后一位有差别,我们只要将两个结点异或再异或1,如果为0,他们就是同一个父结点的子结点。
|
1 2 3 4 5 6 7 8 9 |
inline int ask(int x,int y){ int ans=0; for(x=x+M-1,y=y+M+1;x^y^1;x>>=1,y>>=1){ if(~x&1)ans+=d[x^1];//如果x是左子树,贡献右子树答案 if( y&1)ans+=d[y^1];//如果y是右子树,贡献左子树答案 } return ans; } |
操作二:噩梦的开始——区间修改
例题练习 洛谷P3372
看完上面操作,我相信你能很快写出zkw线段树并且a掉上面的练习,正当你跃跃欲试想要实现区间修改时,一个很不幸的消息:zkw线段树的区间修改版和单点修改版完全不同,连建树都不一样。
具体实现方法有两种,先说差分实现的版本吧。
差分实现区间修改
建树
|
1 2 3 4 5 6 7 8 9 10 |
void build(){//build之前给 N 赋值 for(p=1;p<=n+1;p<<=1); for(int i=1;i<=N;++i) read(S[p+i]); S[p]=P[p]=0; for(int i=N+1;i<p;++i) S[p+i]=0; for(int i=p-1;i>0;--i) S[p+i]-=S[p+i-1];//差分 for(int i=1;i<p;++i) P[p+i]=S[p+i]*i; //计算P for(int i=p-1;i>0;--i) PushUp(i);//建树 } |