题目描述

在一个地区中有 n 个村庄，编号为 1, 2, ..., n。有 n – 1 条道路连接着这些村 庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其 他任一个村庄。每条道路的长度均为 1 个单位。 为保证该地区的安全，巡警车每天要到所有的道路上巡逻。警察局设在编号 为 1 的村庄里，每天巡警车总是从警察局出发，最终又回到警察局。 下图表示一个有 8 个村庄的地区，其中村庄用圆表示（其中村庄 1 用黑色的 圆表示），道路是连接这些圆的线段。为了遍历所有的道路，巡警车需要走的距 离为 14 个单位，每条道路都需要经过两次。

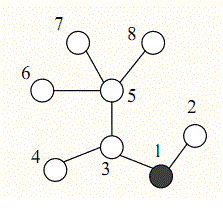
为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路， 每条新道路可以连接任意两个村庄。两条新道路可以在同一个村庄会合或结束 （见下面的图例（c））。 一条新道路甚至可以是一个环，即，其两端连接到同一 个村庄。 由于资金有限，K 只能是 1 或 2。同时，为了不浪费资金，每天巡警车必须 经过新建的道路正好一次。 下图给出了一些建立新道路的例子：

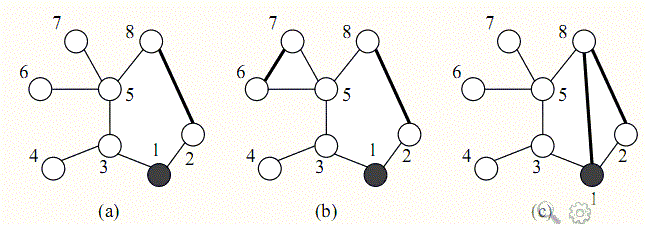
在(a)中，新建了一条道路，总的距离是 11。在(b)中，新建了两条道路，总 的巡逻距离是 10。在(c)中，新建了两条道路，但由于巡警车要经过每条新道路 正好一次，总的距离变为了 15。 试编写一个程序，读取村庄间道路的信息和需要新建的道路数，计算出最佳 的新建道路的方案使得总的巡逻距离最小，并输出这个最小的巡逻距离。

输入输出格式

输入格式：

第一行包含两个整数 n, K(1 ≤ K ≤ 2)。接下来 n – 1 行，每行两个整数 a, b， 表示村庄 a 与 b 之间有一条道路(1 ≤ a, b ≤ n)。

输出格式：

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

输入输出样例

输入样例1：

输出样例1：

输入样例2：

输出样例2：

输入样例3：

输出样例3：

说明

10%的数据中，n ≤ 1000, K = 1；

30%的数据中，K = 1；

80%的数据中，每个村庄相邻的村庄数不超过 25；

90%的数据中，每个村庄相邻的村庄数不超过 150； 100%的数据中，3 ≤ n ≤ 100,000, 1 ≤ K ≤ 2。

---

如果不建边的话，每一条边都要被经过两边，所以答案就是\(2(n-1)\)。
建立一条新的道路后，根据题目意思，新的道路要被经过一次，所以在沿着\((x,y)\)巡逻之后，要返回\(x\)，就必须沿着树上从\(y\)到\(x\)的路径巡逻一遍，最终形成一个环。这个环上的树边对答案的贡献就减一，显然，在树的直径的两端点建边最优。若树的直径为\(L\)答案就是\(2(n-1)-L+1\)。

建两条边，有两个环，如果不重叠，答案继续减小，如果重叠，重叠部分的树边对答案的贡献又会变为2.
我们可以这样来解决这个问题：
1. 在最初的树上求直径，设直径为L1，然后把直径上的边权取反。
2. 在直径边权取反之后的树上再次求直径，设直径为L2.
答案就是\(2(n-1)-(L_1-1)-(L_2-1)=2n-L_1-L_2\)

代码