题目大意：有一棵 n 个节点的树，每条边长度为 1，颜色为黑或白。
可以执行若干次如下操作：选择一条简单路径，反转路径上所有边的颜色。
对于某些边，要求在操作结束时为某一种颜色。
给定每条边的初始颜色，求最小操作数，以及满足操作数最小时，最小的操作路径长度和。

没想到还有人Day3能考285分 orz %%%

这道题看了题解也有点迷（主要是太短了）
感谢@Ajsoabk的指点，感觉懂了很多。

首先我们给出以下定义：

名称	含义
奇度数点-	-拥有奇数度数的翻转边的点
边类型0--	初始状态和目标状态相同
边类型1--	初始状态和目标状态不同
边类型2--	没有要求

我们考虑一颗简单树

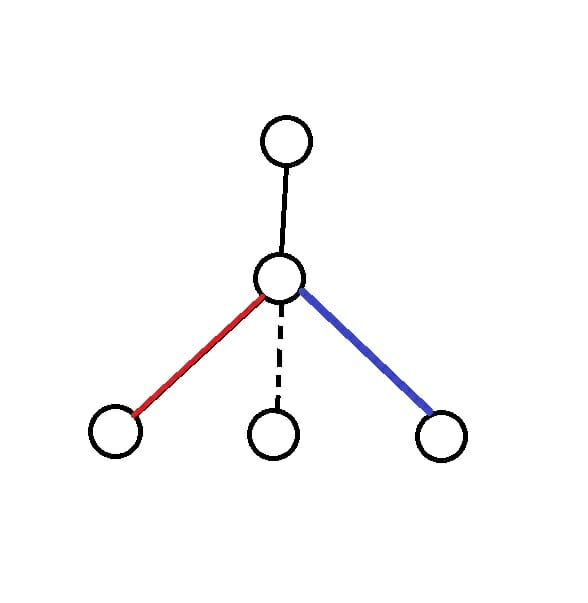
先不考虑父节点，我们可以将边分为3类，分类的标准为 初始颜色xor目标颜色，蓝色粗线（右侧）为0，即初始状态和目标状态相同，红色线（左侧）为1，即初始状态和目标状态不同，黑色虚线（中）为2，即没有要求。

我们可以维护一个二元组，\(dp[i]\)存储i为根的子树内最少的奇度数点数、此时最小总长度。
而我们可以知道的是，无论是哪一条简单路径，都会在两侧端点产生两个奇度数点，而且不会重叠（因为重叠了就可以合并成一步）
于是我们最终的答案就是\(\frac{dp[1].first}{2},dp[1].second\)。

但是如何更新状态呢？
我们可以从叶子节点开始考虑，我们发现如果要更新父节点，就和当前节点与父节点的边的类型有关，如果是类型0，则我们不能翻转它（翻转偶数次也可以满足状态不变，但不是最优解），如果是类型1，我们必须翻转它，如果是类型0，我们可以翻转，也可以不翻转。
因此我们可以在dp数组中加上一维0/1，\(dp[i][0/1]\)储存i与父节点是否翻转的情况下，i为根的子树内最少的奇度数点数、此时最小总长度。

为了更新我们的状态，我们需要额外开两个变量。

变量名	作用
tmp0	储存根节点与所有子节点之间有偶数条边被翻转的情况下，奇度数点的个数和路径长度
tmp1	储存根节点与所有子节点之间有奇数条边被翻转的情况下，奇度数点的个数和路径长度

为什么分奇偶？我们把刚刚的树拓展一下：

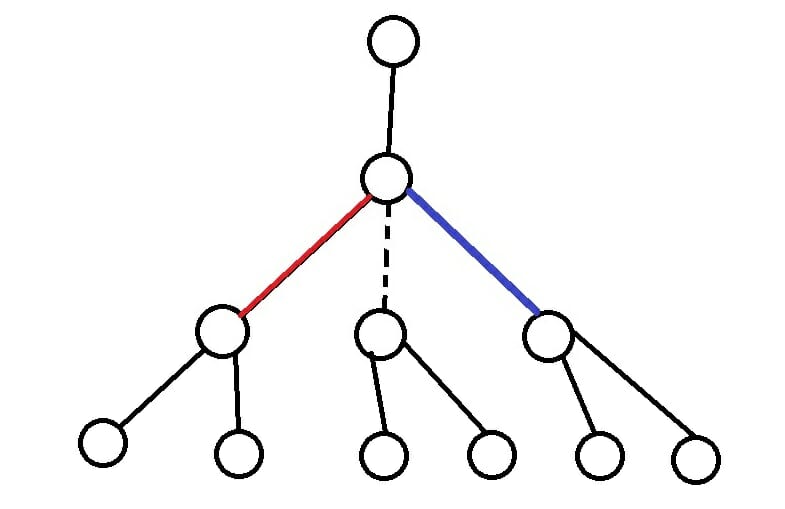
我们现在只考虑叶子节点上一层的节点怎么更新父节点
1. 如果是蓝边或者虚线边，能更新\(dp[i][0]\)，由于没有取这条边，所以i节点的tmp0将被继承到父节点，而tmp1由于是有奇数条边，所以i节点自己就是一个奇度数点，继承到父节点的时候，奇度数点个数要加一。
2. 如果是红边或者虚线边，能更新\(dp[i][1]\)，由于取了这条边，所以i节点的tmp0被继承到父节点时，i节点变为奇度数点，奇度数点+1，路径+1，而tmp1变为偶度数点，奇度数点个数直接继承，路径+1。
3. 没有更新到的状态就为inf

代码