首先这是一颗树。
这一题我们用贪心的方法来解决,首先来看看样例:

样例1很不友好,不如不给,显然我们可以经过3个点。
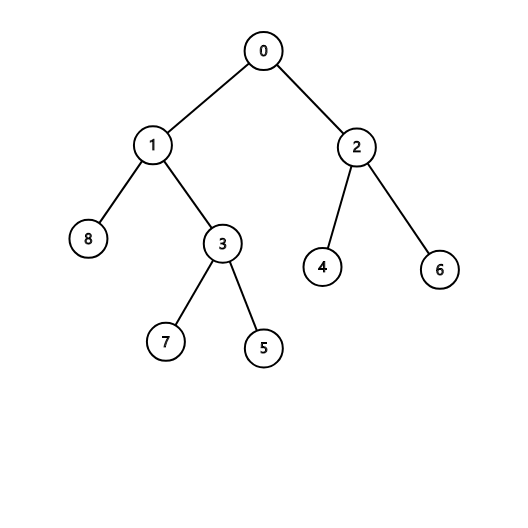
我们可以从样例2发现我们的贪心策略。
为了实现经过的点最多的这一条件,我们希望每次走一步都多走一个点,如果我们选择最长链的话,在链上每走一步就多走了一个点,如果走不完最长链,那答案就是步数+1,而如果走完最长链还有剩余步数的话,每两步可以多访问一个节点。
为什么剩余步数每两步可以多访问一个节点?
对于没有全访问的情况(如果这种方法求出来的值大于总数,则输出总数),最长链上肯定存在一条边连着一个没有访问的节点 ,当走到这里的时候,可以花两步去访问再回来。
为什么最长链是最优的?
显然,因为如果我们不走最长链的话,我们走任意其他的链对答案的贡献都没有最长链大,虽然剩下的剩余步数多,但是根据上面的推论,每两个剩余步数才有一个贡献,因此最长链是最优的。
讲得已经比较清楚了,有些细节没有提到,建议先自己写一遍再看代码!!
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
#include<bits/stdc++.h> using namespace std; const int MAXN = 103; int Nt[MAXN<<1],Head[MAXN<<1],to[MAXN<<1],tot; bool used[MAXN]; int n,m; int mx=0; void add(int a,int b){ Nt[++tot]=Head[a]; to[tot]=b; Head[a]=tot; } void dfs(int pos,int dep){//最长链可以用深搜跑最大深度得到 used[pos]=1; mx=max(mx,dep); for(int i=Head[pos];i;i=Nt[i]){ int y=to[i]; if(used[y])continue; dfs(y,dep+1); } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<n;i++){ int a,b; scanf("%d%d",&a,&b); add(a,b);add(b,a); } dfs(0,1); if(m<=mx-1)printf("%d\n",m+1);//如果走不完最长链,那答案就是步数+1 else printf("%d\n",min(n,mx+(m-mx+1)/2)); return 0; } |