不得不说,网络流的题目其实实现起来都是套模板,但是要想到就很困难。
很多人学了最小割之后就来切这道“裸题”,数据范围小,还没要求输出具体方案,太简单了!
但是最小割是适用于有向图,而且是边集,但是这道题是要我们找出点的个数,而且是无向图。
在看这篇题解的时候默认你知道“最大流最小割定理”
我们先来着手解决第一个问题:无向图转化成有向图。
由于这道题是关于图的连通性的问题,因此转化出来的有向图和原图连通性不变
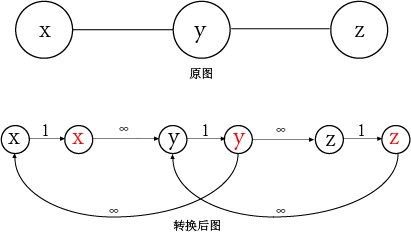
如上图,我们可以将原来的图的每个点,拆成两个点x,x'(图中的点不包括源点和汇点),在它们之间连容量为1的有向边。对于原来的边(x,y),我们可以转化成(x',y)和(y',x)这两条有向边,容量为\(\infty\)
这样做显然连通性不变。
而且,我们发现,在原图中,如果删去y点,x与z就不连通了;
在转换图中,如果删去(y,y')那么x与z也是不连通的;
于是我们可以将问题转化为:在转化后图中,至少删掉多少条权值为1的边才能使图不连通;
这就是一个典型的最小割问题,由于其他边权值都是\infty,而图中最大流量为N-2,因此求最小割的时候贡献答案的一定是权值为1的边。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
#include<bits/stdc++.h> using namespace std; const int MAXN =500; const int inf=1<<30; int Head[MAXN*10],Nt[MAXN*10],val[MAXN*10],to[MAXN*10],pre[MAXN],incf[MAXN],v[MAXN]; int s,t,n,m,tot=1,maxflow; int a[MAXN],b[MAXN]; void add(int x,int y,int z){ Nt[++tot]=Head[x]; to[tot]=y; val[tot]=z; Head[x]=tot; Nt[++tot]=Head[y]; to[tot]=x; val[tot]=0; Head[y]=tot; } int read(){ int x=0,f=1;char ch='['; while(!isdigit(ch)){ch=getchar();if(ch=='-')f=-1;} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x*f; } bool bfs(){ memset(v,0,sizeof(v)); queue<int>q; q.push(s);incf[s]=inf;v[s]=1; while(q.size()){ int x=q.front();q.pop(); for(int i=Head[x];i;i=Nt[i]){ if(val[i]){ int y=to[i]; if(v[y])continue; incf[y]=min(incf[x],val[i]); pre[y]=i; if(y==t)return 1; q.push(y);v[y]=1; } } } return 0; } void update(){ int x=t; while(x!=s){ int i=pre[x]; val[i]-=incf[t]; val[i^1]+=incf[t]; x=to[i^1]; } maxflow+=incf[t]; } int main(){ while(scanf("%d%d",&n,&m)!=EOF){ for(int i=1;i<=m;i++){ a[i]=read()+1; b[i]=read()+1; } int ans=inf; for(s=1;s<=2;s++) for(t=1;t<=n;t++){ if(s!=t){ memset(Head,0,sizeof(Head)); tot=1;maxflow=0; for(int i=1;i<=n;i++){ if(i==s||i==t)add(i,i+n,inf); else add(i,i+n,1); } for(int i=1;i<=m;i++){ add(a[i]+n,b[i],inf); add(b[i]+n,a[i],inf); } while(bfs())update(); ans=min(ans,maxflow); } } if(n<=1||ans==inf)ans=n; cout<<ans<<endl; } return 0; } |
Q&A
对于上面有些问题没弄懂的可以看这里
Q1:为什么最大流量是N-2?
A:你可以想一下最大流量的情况,就是整个图分3层,第一层为源点,第三层为汇点,第二层有N-2个点,每个点流量都是1;
欢迎提问~