题解
这个淀粉质点分治有点意思,与其他的点分治的题目不同的是,这题目并没有让你费劲心思怎么去用log的复杂度进行内层的统计,而是让你想到如何确定当前答案是否最优。
(下面不会讨论点分治的具体实现,此题不适合作为点分治入门题)
在此我们可以将情况分为两种:
1. 点对内
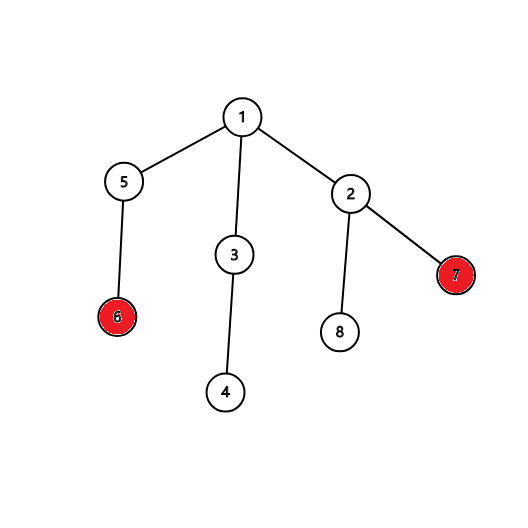
如图,我们的树长这样(假设边权全部为1),标红的是一对点对(6,7),当前的根为1
现在的问题是,当前求出来的答案 ans=4 是最优答案吗?
是!
显然如果如果往2或5走并不会影响答案,而往其他子树走,答案都要增加。
这时输出最优答案
(开始复读)
- 点对间
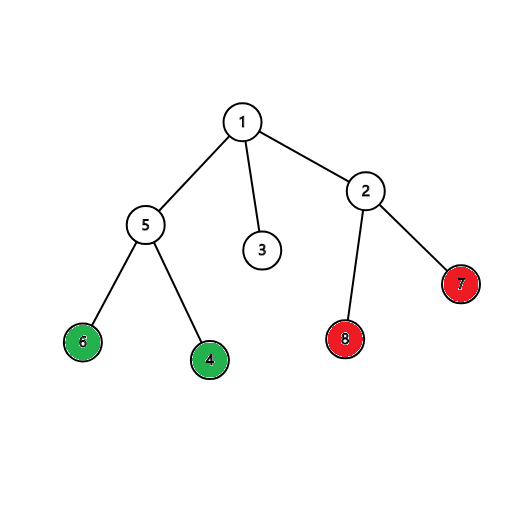
如图,我们的树长这样(假设边权全部为1),标红的是一对点对(8,7),标绿的是另一对(6,4),当前的根为1
现在的问题是,当前求出来的答案 ans=6 是最优答案吗?
是!
显然如果如果往绿点或5红点走并不会影响答案,而往其他子树走,答案都要增加。
这时输出最优答案
(复读结束)
但是还没完,就刚刚两个点对的那幅图来说,我们显然不希望走没有点对经过的边,因此你可以看到 solve 函数中最后并没有对每个子树都递归。
代码
代码有点虚长,都是假的^_^
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 |
#include<bits/stdc++.h> using namespace std; const int N=200003,M=290003; int Head[N],to[M],val[M],Nt[M],tot; int size[N],d[N],b[N]; bool v[N],w[N]; pair<int,int>points[N]; int n,m; int root,now_part,ans=2147483647; struct Tstack{ int num[N],p; int top(){ return num[p]; } void pop(){ p--; } void push(int x){ num[++p]=x; } void clear(){ p=0; } int size(){ return p; } }s; int read(){ int x=0,f=1;char ch=getchar(); while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();} while(isdigit(ch)){x=x*10+ch-'0';ch=getchar();} return x*f; } void add(int x,int y,int z){ Nt[++tot]=Head[x]; to[tot]=y; val[tot]=z; Head[x]=tot; } void find_root(int x,int S){ v[x]=1;size[x]=1;int max_part=0; for(int i=Head[x];i;i=Nt[i]){ int y=to[i]; if(v[y]||w[y])continue; find_root(y,S); size[x]+=size[y]; max_part=max(size[y],max_part); } max_part=max(max_part,S-size[x]); if(max_part<now_part){ now_part=max_part; root=x; } } void dfs(int x,int fa,int rt){ b[x]=rt; for(int i=Head[x];i;i=Nt[i]){ int y=to[i]; if(y==fa)continue; d[y]=d[x]+val[i]; dfs(y,x,rt); } } void solve(int x){ if(w[x]){ printf("%d\n",ans); exit(0); } w[x]=1; d[x]=0; for(int i=Head[x];i;i=Nt[i]){ int y=to[i]; d[y]=val[i]; dfs(y,x,y); } int maxx=0,last=0; for(int i=1;i<=m;i++){ int x=points[i].first,y=points[i].second; if(d[x]+d[y]>maxx){ maxx=d[x]+d[y]; s.clear(); s.push(i); } else if(d[x]+d[y]==maxx){ s.push(i); } } ans=min(ans,maxx); while(s.size()){ int i=s.top();s.pop(); int x=points[i].first,y=points[i].second; if(b[x]!=b[y]){printf("%d\n",ans);exit(0);}//in points else if(!last)last=b[x]; else if(last!=b[x]){printf("%d\n",ans);exit(0);}//between points } memset(v,0,sizeof(v)); now_part=2147483647; find_root(last,size[last]); solve(root); } int main(){ n=read();m=read(); for(int i=1;i<n;i++){ int x,y,z; x=read(); y=read(); z=read(); add(x,y,z); add(y,x,z); } for(int i=1;i<=m;i++){ int x,y; x=read();y=read(); points[i]=make_pair(x,y); } now_part=2147483647; find_root(root=1,n); solve(root); return 0; } |