题解
看到这个首发平台就觉得是rainbowcat出的题,一看题面——都有Freda了,就确定是rainbowcat出的了。
这一题第一次写我写挂了orz
由于与运算和或运算在每一位上都是独立的,我们可以考虑对每一位进行计算。
我们先考虑与运算(其实两个运算是一样的)
于是就成了一个求一个矩阵中,有多少个0/1子矩阵,我们可以考虑用单调栈做。
有一个显然的结论
在一个 N\times M 的矩阵中,以(n,m)为右下角的子矩阵共有 N\times M 个
具体来讲,我们要求出一个s二维数组,s[i][j]表示(i,j)点上方有多少个连续的1,O(N^2)预处理
枚举每一个点,我们来计算以它为右下角的子矩阵个数,观察如下矩阵:
|
1 2 3 4 |
0 0 1 0 0 1 0 1 1 -> 0 1 2 1 1 1 1 2 3 |
假设我们现在统计到(3,3),可以发现它的贡献=(3,2)处贡献+s[3][3] (与前面的组合+该列的组合)
但是,如果是这样一个矩阵:
|
1 2 3 4 |
1 0 0 1 0 0 1 1 0 -> 2 1 0 1 1 1 3 2 1 |
(3,3)处的贡献=(3,2)处的贡献+s[3][3]-1 (1为非法矩阵的数目)
对于一般情况,在2处,A区域就没有意义,4处,B区域就没有意义
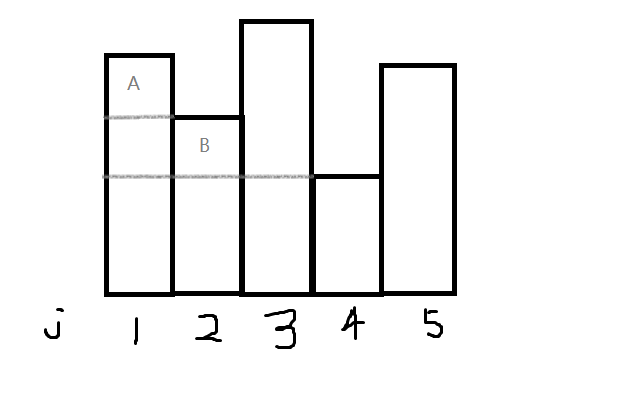
所以我们要维护一个单调栈,栈中元素k要满足s[i][k]单调递增(栈顶s[i][k]最大)
每次有元素出栈时,说明有部分答案不能产生贡献,见代码注释
对于或运算,求所有0子矩阵,全集-0子矩阵数目即是贡献。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int MAXN=2003,mod=1e9+7; int ma[MAXN][MAXN]; int s[MAXN][MAXN]; int stk[MAXN],top; int n; ll ans1,ans2; int main(){ cin>>n; for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ scanf("%d",&ma[i][j]); } } for(int k=0;k<31;k++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ if((ma[i][j]>>k)&1)s[i][j]=s[i-1][j]+1; else s[i][j]=0; } } for(int i=1;i<=n;i++){ ll ans=0;top=0; for(int j=1;j<=n;j++){ ans+=s[i][j]; while(top&&s[i][stk[top]]>=s[i][j]){ ans-=(stk[top]-stk[top-1])*(s[i][stk[top]]-s[i][j]); //栈顶对于第二大的元素的距离×栈顶与j的落差,即为上图中j=3时灰色线的上半部分 top--; } ans1+=ans<<k; ans1%=mod; stk[++top]=j; } } } cout<<ans1<<" "; for(int k=0;k<31;k++){ for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ if((ma[i][j]>>k)&1)s[i][j]=0; else s[i][j]=s[i-1][j]+1; } } for(int i=1;i<=n;i++){ ll ans=0;top=0; for(int j=1;j<=n;j++){ ans+=s[i][j]; while(top&&s[i][stk[top]]>=s[i][j]){ ans-=(stk[top]-stk[top-1])*(s[i][stk[top]]-s[i][j]); top--; } ans2+=(i*j-ans)<<k; ans2%=mod; stk[++top]=j; } } } cout<<ans2<<endl; return 0; } |