题目
题目描述
猫猫TOM和小老鼠JERRY最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。最近,TOM老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中ai>aj且i<j的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。
输入格式
第一行,一个数n,表示序列中有n个数。
第二行n个数,表示给定的序列。
输出格式
给定序列中逆序对的数目。
输入样例
|
1 2 3 |
6 5 4 2 6 3 1 |
输出样例
|
1 2 |
11 |
说明
对于50%的数据,n≤2500
对于100%的数据,n≤40000。
题解
树状数组
既然名字都叫树状数组,那么肯定是和数有关的咯,我们来先看一个二叉树

我们来稍微变下形
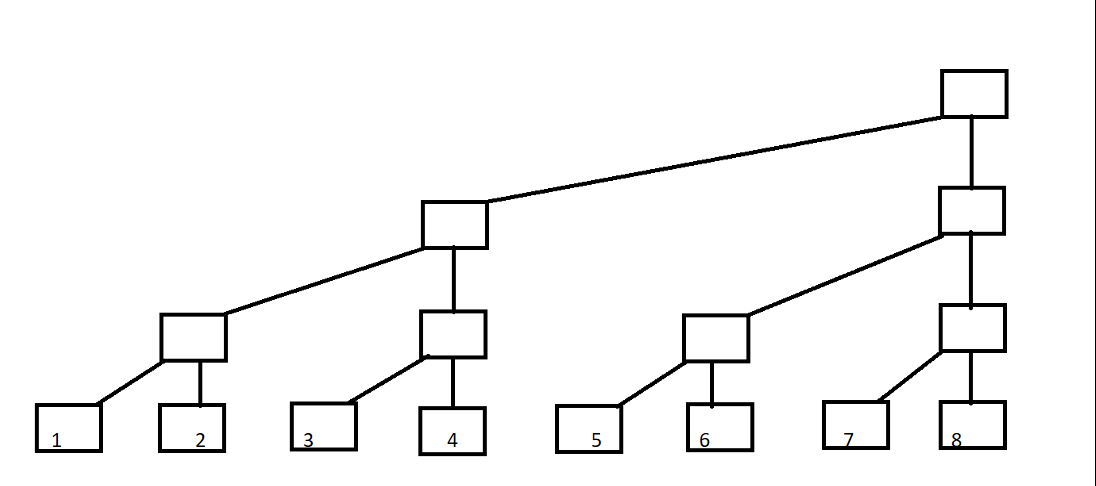
现在我们把树状数组c[]摆放到每一列的顶端
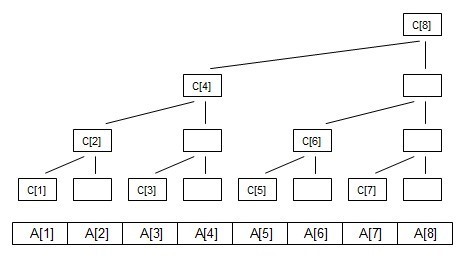
C[i]代表子树的叶子结点的权值之和
我们通过这张图可以知道
C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
C[5]=A[5];
C[6]=A[5]+A[6];
C[7]=A[7];
C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
通过分情况讨论好像是有什么规律,那有没有更一般的规律呢?
我们不妨将树状数组的编号转换成二进制看看
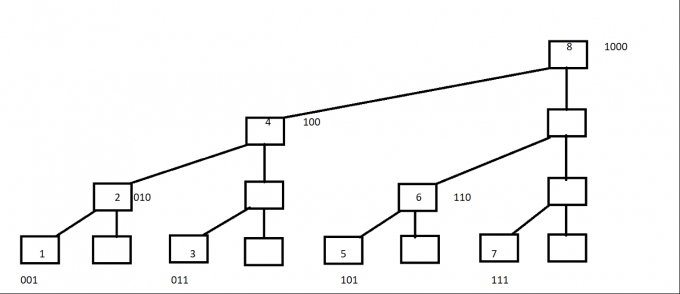
1=(001)---C[1]=A[1];
2=(010)---C[2]=A[1]+A[2];
3=(011)---C[3]=A[3];
4=(100)---C[4]=A[1]+A[2]+A[3]+A[4];
5=(101)---C[5]=A[5];
6=(110)---C[6]=A[5]+A[6];
7=(111)---C[7]=A[7];
8=(1000)---C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];
对照式子可以发现 C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; (k为i的二进制中从最低位到高位连续零的长度)例如i=8时,k=3。
而lowbit(x)函数的作用就是取出x的最低位。
树状数组的优点在于单点更新以及区间查询,对于求逆序对来说,知道一个数的位置x,那么1~x范围内就是比它小的数,而用已经插入的数的个数减去这个数,累加起来就是我们要算的逆序对数。
离散化
上面提到我们要知道一个数的位置,可以用树状数组下标来表示c[x],但整型范围很大,不可能开这么大的数组,所以我们只需要保留它们的相对大小,用离散化处理。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define MAXN 100001 using namespace std; int n; struct node{ int num,index; }a[MAXN]; int c[MAXN];//树状数组 int A[MAXN];//离散化后的数组 int low_bit(int i) { return i&(-i); } void update(int i,int v)//插入 { while(i<=n){ c[i]+=v; i+=low_bit(i); } } int get_sum(int i)//区间查找 { int res=0; while(i){ res+=c[i]; i-=low_bit(i); } return res; } bool cmp(node a,node b) { return a.num<b.num; } int main(){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i].num); a[i].index=i; } sort(a+1,a+1+n,cmp); int p=0; for(int i=1;i<=n;i++){ /*if(a[i].num!=a[i-1].num)p++; A[a[i].index]=p;*///如果数据中存在重复数据才需要 A[a[i].index]=i;//离散化 } long long ans=0; for(int i=1;i<=n;i++){ update(A[i],1);//插入 ans+=i-get_sum(A[i]); } printf("%lld",ans); return 0; } |