题目
题目描述
求有多少种长度为 n 的序列 A,满足以下条件:
1 ~ n 这 n 个数在序列中各出现了一次
若第 i 个数 A[i] 的值为 i,则称 i 是稳定的。序列恰好有 m 个数是稳定的
满足条件的序列可能很多,序列数对 10^9+7 取模。
输入格式
第一行一个数 T,表示有 T 组数据。
接下来 T 行,每行两个整数 n、m。
T=500000,n≤1000000,m≤1000000
输出格式
输出 T 行,每行一个数,表示求出的序列数
输入样例
|
1 2 3 4 5 6 7 |
5 1 0 1 1 5 2 100 50 10000 5000 |
输出样例
|
1 2 3 4 5 6 |
0 1 20 578028887 60695423 |
题解
没思路?我们来找规律!
比如一个\(n=5\)的排列,我们假设\(m=2\)也就是说,我们其实已经确定了排列种某些位置的值,就这个例子来说:
\(12???\) \(1?3??\) \(1??4?\) \(1???5\) \(?23??\) \(?2?4?\) \(?2??5\) \(??34?\) \(??3?5\) \(???45\)
共10种,很容易发现其实就是\(C_n^m\),那么其中的问号又多少种排列呢?
没思路?我们再来找规律!
我们设\(D_i\)为i个?的可能的排列数,显然,\(D_1=0\) \(D_2=1\)
接着我们来看下\(D_3\),可以有\(312\),\(231\)
如果我们继续找下去的话,容易出错,所以我们现在来找找规律(灵魂画师)。
就拿\(D_4\)来说,上面的是数,下面的是位置,首先,1不能放到1号位,而且放到2,3,4上对于递推是等价的,于是他别无选择地放到了其他地方(假设是2号位)
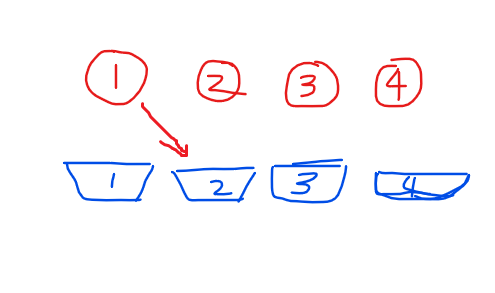
然后我们假设2放到1号位上去,剩下的3,4正好是\(D_2\)
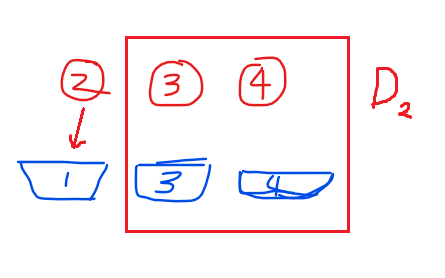
但2怎么可能只有放在1号位上的命运呢?它还可以不放到1号位,咦?我们之前说,i不能放到i号位,那么既然2不放到1号位,那么1号位在这里是不是等价于2号位呢?没错!
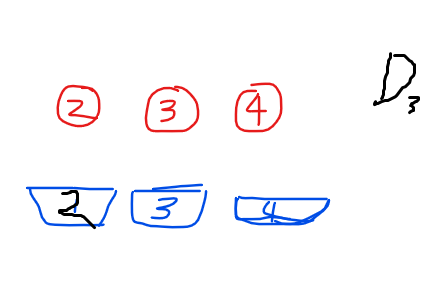
而之前的“万恶之源”数字1,它有\(n-1\)种放法,所以我们就大胆猜测:\(D_n=(n-1)(D_{n-1}+D_{n-2})\)
严谨的证明还请大家自己百度
然后我们就愉快地输出\(C_n^m\times D_{n-m}\)就好啦
其他知识点比如说逆元求组合数(费马小定理)还请大家自行了解
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
#include<iostream> #include<cstdio> using namespace std; typedef long long ll; const int MAXN=1000005,mod=1000000007; ll f[MAXN],inv[MAXN],d[MAXN]; int t; ll qpow(ll a,ll b){ ll ans=1; while(b){ if(b&1)ans=a*ans%mod; a=a*a%mod; b>>=1; } return ans; } void prework(){ f[0]=1; for(int i=1;i<MAXN;i++){ f[i]=f[i-1]*i%mod; inv[i]=qpow(f[i],mod-2); } d[1]=0,d[2]=1,d[3]=2; for(int i=4;i<MAXN;i++){ d[i]=(i-1)*(d[i-1]+d[i-2])%mod; } } int main(){ cin>>t; prework(); for(int i=1;i<=t;i++){ ll n,m; scanf("%lld%lld",&n,&m); if (n - m == 1) printf("0\n"); else if (m == n) printf("1\n"); else if (m == 0) printf("%lld\n",d[n]); else { printf("%lld\n",f[n] * inv[m] % mod * inv[n-m] % mod * d[n-m] % mod); } } return 0; } |