阅读量:1,061 views
题目
题目描述
给定长度为N的数列A,以及M条指令 (N≤500000, M≤100000),每条指令可能是以下两种之一:
“2 x y”,把 \(A[x]\) 改成 \(y\)。
“1 x y”,查询区间 \([x,y]\) 中的最大连续子段和,即 \(max(x≤l≤r≤y) { \sum_{l\le i \le r} A[i] }\)。
对于每个询问,输出一个整数表示答案。
输入
第一行两个整数N,M
第二行N个整数Ai
接下来M行每行3个整数k,x,y,k=1表示查询(此时如果x>y,请交换x,y),k=2表示修改
输出
对于每个询问输出一个整数表示答案。
样例输入
|
1 2 3 4 5 6 |
5 3 1 2 -3 4 5 1 2 3 2 2 -1 1 3 2 |
样例输出
|
1 2 3 |
2 -1 |
提示
数据范围与约定
对于100%的数据: N≤500000, M≤100000, |Ai|<=1000
题解
树存储空间大小
这道题与原题略微有点区别,数据输入顺序不一样,以及范围更大了,但是稍微改一下就可以过了。
第一个问题,为什么树要开到4*N?
首先,我们构造的线段树有可能是完全二叉树(最好情况),叶子节点存储的就是我们每一个点的数据,而我们可以分析下完全二叉树的图。
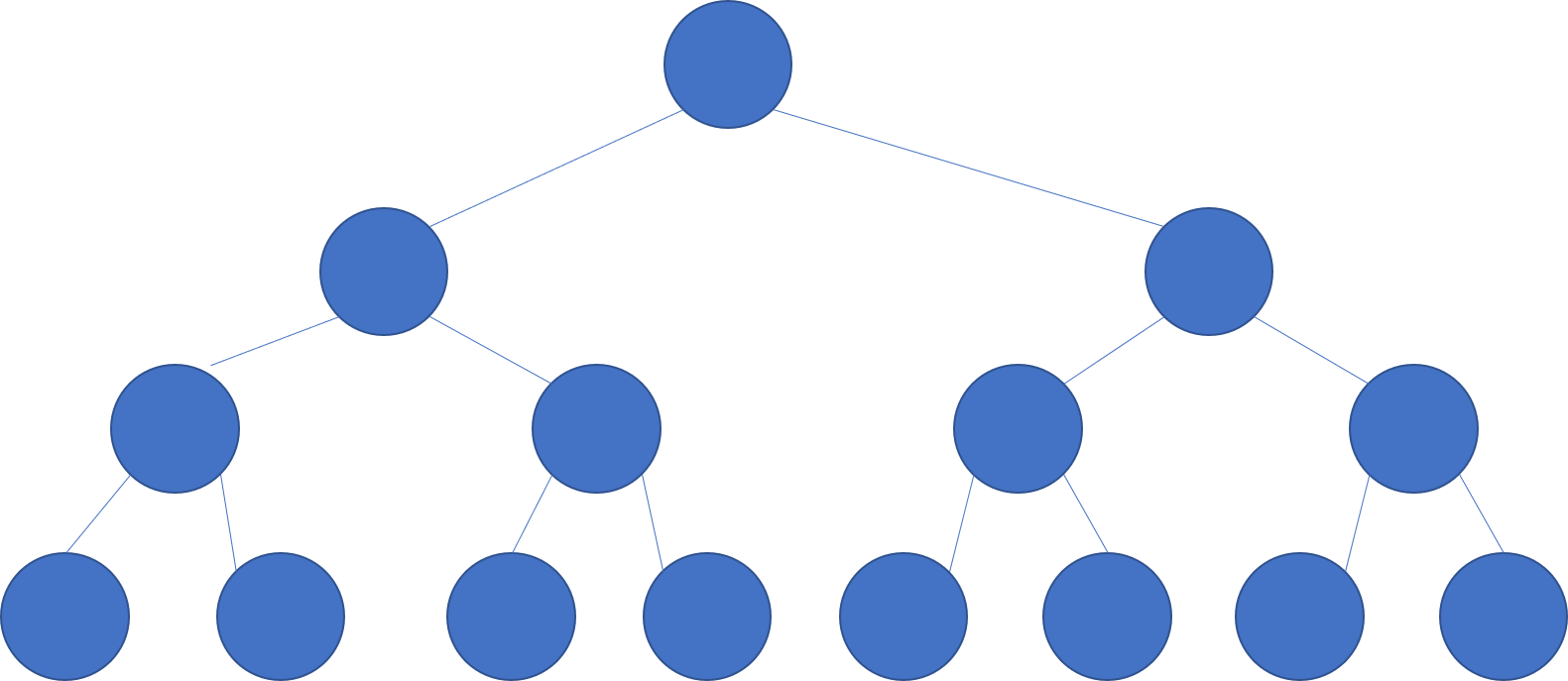
不难发现,我们设节点有n个,那么二叉树的层数为\( log_2(n+1) \)
而设叶子节点有k个,那么就得到一个k与n的关系:\( k(1-(1/2)^n)=2n \)
n随k的变化关系曲线为
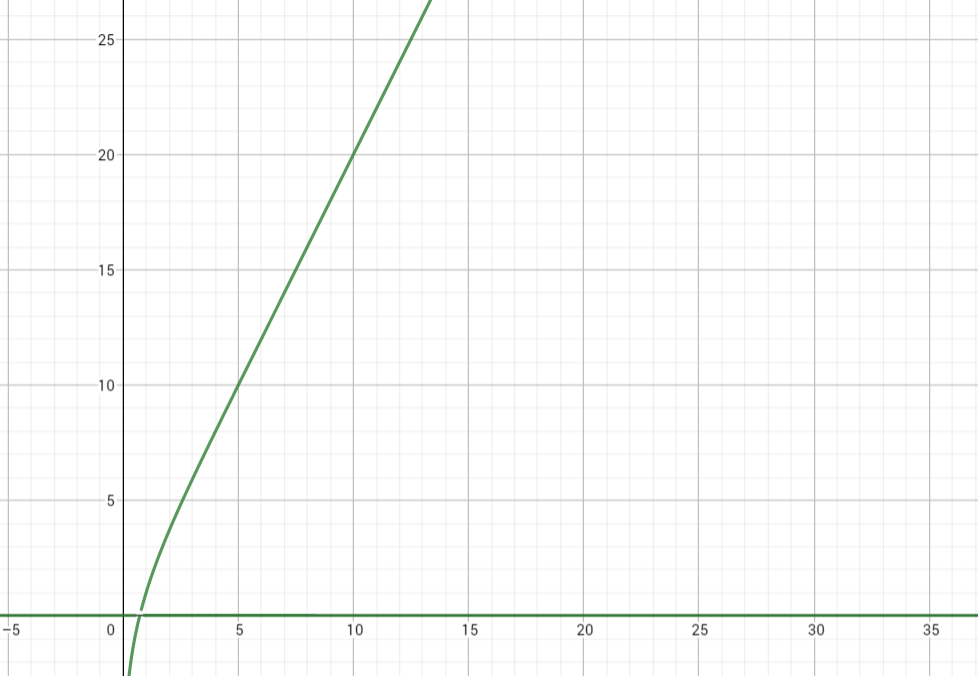
当k趋于无穷大,\(n=2k\)
而对于最坏情况,请参见这篇文章
对于最坏的情况我们要开4n的空间来存储。
树存储方式
第二个问题,我们要存树,这里可以开一个结构体,里面有四个变量
| 变量名称 | 变量作用 |
|---|---|
| data | 储存该区间内的最大连续子段和 |
| ldata | 储存该区间从左端开始的最大和 |
| rdata | 储存该区间从右端开始的最大和 |
| sum | 储存该区间内的所有数的和 |
这些就够了,不必纪录左子树和右子树。
建树
对于每个叶子节点(r==l),我们给他们赋值,而其他节点我们就需要来分析情况了。
sum的值
sum的值还用说吗,就是左子树的sum+右子树的sum
data的值
data是该区间内的最大连续子段和,所以对于data就有几种可能,而我们要做的就是取最大的:
1.data=左子树data
2.data=右子树data
3.data=左子树rdata+右子树ldata
ldata和rdata的值
ldata储存该区间从左端开始的最大和,所以:
1.ldata=左子树ldata
2.ldata=左子树sum+右子树rdata
rdata同理
改变值
改变值其实就是建树,只不过因为只改变一个值,所以分治时要么是左子树,要么是右子树,改变完后要注意重新维护其他点的值。
查询值
查询值较为复杂,但我们也可以把它看成一个建树的过程。
首先,对于我们要查询的范围,如果这个范围大于等于我们分治下去的范围,那么就返回这个范围的值。(实际上就是我们建树时存在这个范围的点)
如果这个范围没有点满足,那么我们可以用叶子节点建树来建成我们想要的范围的点。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
#include<iostream> #include<cstdio> #include<cstring> using namespace std; #define MAXN 500000 struct Ttree{ int data; int ldata,rdata; int sum; }t[MAXN*4],tmp0; int n,m; void push_up(int l,int r,int k){ t[k].sum=t[k*2].sum+t[k*2+1].sum; t[k].data=max(t[k*2].data,t[k*2+1].data); t[k].data=max(t[k*2].rdata+t[k*2+1].ldata,t[k].data); t[k].ldata=max(t[k*2].ldata,t[k*2].sum+t[k*2+1].ldata); t[k].rdata=max(t[k*2+1].rdata,t[k*2+1].sum+t[k*2].rdata); return; } void make(int l,int r,int k){ if(l==r){ scanf("%d",&t[k].data); t[k].ldata=t[k].rdata=t[k].sum=t[k].data; return; } int mid=(l+r)/2; make(l,mid,k*2); make(mid+1,r,k*2+1); push_up(l,r,k); return; } Ttree ask(int L,int R,int l,int r,int k){ if(L<=l&&r<=R)return t[k]; int mid=(l+r)/2; Ttree res1; if(L<=mid)res1=ask(L,R,l,mid,k*2); else res1=tmp0;/*目前分治的点的左子树不包含要查询的左端范围,不参与建树,tmp0初始化很小,在取最大值的时候含有它的情况会被忽略掉,但是tmp0.sum初始化还是0*/ Ttree res2; if(R>mid)res2=ask(L,R,mid+1,r,k*2+1); else res2=tmp0;//同理 Ttree res={0}; res.sum=res1.sum+res2.sum; res.data=max(res1.data,res2.data); res.data=max(res1.rdata+res2.ldata,res.data); res.ldata=max(res1.ldata,res1.sum+res2.ldata); res.rdata=max(res2.rdata,res2.sum+res1.rdata); return res; } void change(int x,int y,int l,int r,int k){ if(l==r){ t[k].data=y; t[k].ldata=t[k].rdata=t[k].sum=t[k].data; return; } int mid=(r+l)/2; if(x<=mid)change(x,y,l,mid,k*2); else change(x,y,mid+1,r,k*2+1); push_up(l,r,k); return; } int main(){ tmp0.data=tmp0.ldata=tmp0.rdata=-1e9; scanf("%d%d",&n,&m); make(1,n,1); for(int i=1;i<=m;i++){ int k,x,y; scanf("%d%d%d",&k,&x,&y); if(k==1){ if(x>y)swap(x,y); printf("%d\n",ask(x,y,1,n,1).data); }else{ change(x,y,1,n,1); } } return 0; } |