题目
题目背景
某个局域网内有n(n<=100)台计算机,由于搭建局域网时工作人员的疏忽,现在局域网内的连接形成了回路,我们知道如果局域网形成回路那么数据将不停的在回路内传输,造成网络卡的现象。因为连接计算机的网线本身不同,所以有一些连线不是很畅通,我们用f(i,j)表示i,j之间连接的畅通程度,f(i,j)值越小表示i,j之间连接越通畅,f(i,j)为0表示i,j之间无网线连接。
题目描述
需要解决回路问题,我们将除去一些连线,使得网络中没有回路,并且被除去网线的Σf(i,j)最大,请求出这个最大值。
输入格式
第一行两个正整数n k
接下来的k行每行三个正整数i j m表示i,j两台计算机之间有网线联通,通畅程度为m。
输出格式
一个正整数,Σf(i,j)的最大值。
输入样例
|
1 2 3 4 5 6 7 |
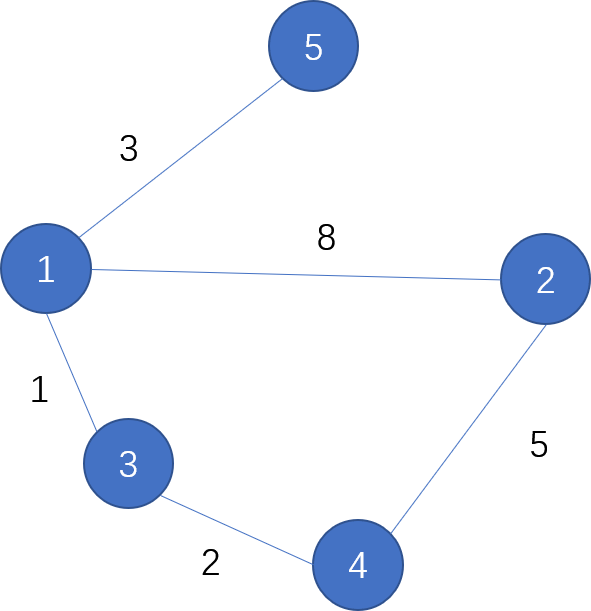
5 5 1 2 8 1 3 1 1 5 3 2 4 5 3 4 2 |
输出样例
|
1 2 |
8 |
说明
f(i,j)<=1000
题解
这里可以采用存边的方法存储图,再用克鲁斯卡尔按边求出最小生成树,把这些边标记起来,再把没有标记过的相加,这样做的好处是避免数据溢出(当然你也可以开长整型)
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; struct Tedge { int from; int to; int num; }edge[10001]; int father[101];//并查集 bool Ebook[10001]; int n,k,ans; int find(int x){ if(x==father[x])return x; return find(father[x]);//这里一定要有return } void solve(){ for(int i=1;i<=k;i++){ int f1,f2; f1=find(edge[i].from); f2=find(edge[i].to); if(f1!=f2){ father[f1]=f2; Ebook[i]=1; } } } bool cmp(Tedge a,Tedge b){ return a.num<b.num; } int main(){ scanf("%d%d",&n,&k); for(int i=1;i<=n;i++)father[i]=i; for(int i=1;i<=k;i++){ scanf("%d %d %d",&edge[i].from,&edge[i].to,&edge[i].num); } sort(edge+1,edge+k+1,cmp);//求最小生成树,边由小到大 solve(); for(int i=1;i<=k;i++)if(Ebook[i]==0)ans+=edge[i].num; cout<<ans; return 0; } |