T1 不老的传说
题目大意:有n个石头环成一圈,每次染色能染1-k个连续石头,问多最少多少次能染成目标状态
这道题真的是各种既视感,环的话直接变成两倍的链就OK了,之后就是区间dp
\(f[i][j]\)表示(i,j)对i,j一段染色的最少次数
初始化就是\(f[i][j]=\begin{cases}1&i=j\\ 0&i>j\\ \infty&else\end{cases}\)
状态转移方程也很有既视感:\(f[i][j]=\begin{cases}min(f[i+1][j],f[i][j-1])&c[i]=c[j]\\min(f[i][z]+f[z+1][j]),z\in [i,j)&else\end{cases}\)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
#include<bits/stdc++.h> using namespace std; int c[402]; int f[402][402]; int n,m,k; int main(){ scanf("%d%d%d",&n,&m,&k); memset(f,0x3f,sizeof(f)); for(int i=1;i<=n;i++){scanf("%d",&c[i]);c[i+n]=c[i];} for(int i=1;i<=n*2;i++){ for(int j=1;j<=n*2;j++){ if(i==j)f[i][j]=1; if(i>j)f[i][j]=0; } } for(int len=2;len<=n;len++){ for(int i=1;i+len-1<=n*2;i++){ int j=i+len-1; if(c[i]==c[j]&&len<=k)f[i][j]=min(f[i+1][j],f[i][j-1]); else { for(int z=i;z<j;z++){ f[i][j]=min(f[i][z]+f[z+1][j],f[i][j]); } } } } int mi=1<<30; for(int i=1;i<=n;i++){ mi=min(mi,f[i][i+n-1]); } cout<<mi<<endl; return 0; } |
T2 多米诺骨牌
题目要求的是上下翻转次数,首先要解决的是如何使得差值最小。很容易就这样想到,因为n块骨牌都可以任意翻转,那么肯定有一种摆放的方式顶行和底行之间的差值是最小的,找到这样的摆放方式就可以通过对比找到最小的翻转次数了,但是这样一个问题也不容易解决,因为总共有2n种摆放方式,不可能用计算机逐一检验对比。而且差值最小的摆放方式也不惟一,因此这样的方法是不可行的。
这个问题只能换一种方式来解决了。我们可以尝试一下动态规划的思想。之所以往这个方向去思考是因为我们发现,上面的方法行不通的主要原因是因为骨牌之间相互独立的,这个性质导致了摆放方式有很多,但是相互独立这个很重要的性质,如果能够加以利用,也许会为问题的解决带来很大的便利。
经过分析可以发現,如果做到了用最少的翻转次数达到差值是最小的摆放方式,此时任意一段骨牌都不可能用更少的方式得到同样的上下差值。更具体地说,前k块骨牌如果要达到某个差值(不一定最小),它将取决于前1块的翻转情况和第k块的翻转情况。如果确定了第k块的状态,那么前k-1块就必须要用最少的次数得到指定的差值了。据此,可以列出下面的递推公式:
假设gap[i][j]表示前i块骨牌要达到差值为j,需要的最少翻转次数。如果不能达到j的差值,那么令等于一个很大的数。
\(gap[i][j]=\begin{cases}min(gap[i-1][j-c[i]],gap[i-1][j+c[i]]+1),i\in [1,n] \\ \infty & else\end{cases}\)
其中c[i]为第i个骨牌上面-下面的值
初始条件是:
\(\begin{cases}g[0][0]=0\\g[0][j]=\infty\end{cases}\)
由于最多只有1000个骨牌,所以上下骨牌点数差值的总和的绝对值最大就是5000。所以,我们可以逐个骨牌来处理,把所有可以达到的值都计算出来,并记下是用了多少步而达到的,最后找出可以达到的最小值,并直接得到需要多少步达到。这样可以在规定时间内求得答案。
由于上下的差值在\([-5000,5000]\)之间,所以我们gap的第二维要开两倍空间,再往右偏移一倍空间
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#include<bits/stdc++.h> using namespace std; int gap[1003][12012]; int c[1003]; int n; int main(){ cin>>n; for(int i=1;i<=n;i++){ int a,b; scanf("%d%d",&a,&b); c[i]=a-b; } memset(gap,0x3f,sizeof(gap)); gap[0][6005]=0; for(int i=1;i<=n;i++){ for(int j=0;j<12100;j++){ if(j-(c[i])>=0 && j-(c[i])<12100) gap[i][j]=min(gap[i][j], gap[i-1][j+c[i]]);//虽然我们上面把它们写到了一起, if(j+c[i]>=0 && j+c[i]<12100) gap[i][j]=min(gap[i][j], gap[i-1][j-c[i]]+1);//但实际上它们两个更新的条件是不一样的,所以要分开来写 } } int minn=0x3f3f3f3f,ans=0x3f3f3f3f; for(int i=0;i<12100;i++) { if(gap[n][i]!=0x3f3f3f3f) { if(abs(i-6005)<minn) minn=abs(i-6005), ans=gap[n][i]; else if(abs(i-6005)==minn) ans=min(ans, gap[n][i]); } } cout<<ans<<endl; return 0; } |
T3 文本压缩
题目大意:给你一个字符串和若干编码方式,输出编码后的最小长度
题目中的编码有个特点,就是无后效性,如abcdefgh前面的abcd如何编码跟后面的编码方法无关。
设函数\(F(s)\)表示文本s的压缩方式的编码长度,如题目例子:
\(F(a)=length("01")=2\)
\(F(abc)=length("0")=1\)
\(F(abcd)=4\)
\(F(bcd)=1\)
\(F(def)=2\)
\(F(ef)=2\)
设函数\(G(s)\)表示文本s的最短编码长度,有
\(G(a)=2\)
\(G(ab)=max\)
\(G(abc)=1\)
\(G(abcd)=4\)
\(G(abcde)=max\)
max表示不能编码
求\(G(abcdef)\)时,考虑其最后一个编码可能是def或ef,即abcdef=abc+def或abcd+ef
转移方程为:
\(G(s)=min(G(s_{11})+F(s_{12}),G(s_{21})+F(s_{22}),\cdots ,G(s_{n1})+F(s_{n2}))\)
其中\(s=s_{i1}+s_{i2},i\in[1,n]\)
@千柰dalao只开了1维数组,代码也比我的简洁
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
#include<bits/stdc++.h> using namespace std; string s; string v[502];//好像没什么用,根本不用开数组 map<string,int>len;//就是上面的f数组 int f[503][503]; int get(int l,int r){ string tmp; for(int i=l;i<=r;i++){ tmp+=s[i]; } if(len[tmp]){return len[tmp];} else return 0x3f3f3f3f; } int main(){ int t;cin>>t; while(t--){ s.clear();len.clear(); memset(f,0x3f,sizeof(f)); int tot=0; cin>>s;scanf("\n"); while(cin.peek()=='('){//毒瘤读入,不要学我 cin>>v[++tot];int p=1,cnt=0; string tmp2; while(v[tot][p]!=',')tmp2+=v[tot][p++]; p++; while(v[tot][p]!=')'){cnt++;v[tot][p++];} len[tmp2]=cnt; if(cin.peek()==EOF)break; scanf("\n"); } for(int i=0;i<s.length();i++){//先处理出给出了编码的 for(int j=i;j<s.length();j++){ f[i][j]=get(i,j); } } for(int l=2;l<=s.length();l++){//区间dp for(int i=0;i+l-1<s.length();i++){ int j=i+l-1; for(int k=i;k<j;k++){ f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]); } } } if(f[0][s.length()-1]==0x3f3f3f3f)printf("0\n"); else printf("%d\n",f[0][s.length()-1]); } return 0; } |
T4 瑞士轮
dp专题出现排序算法真的是一点也不意外呢,当时还在努力想怎么dp,还好最后打了个暴力,没有被坑惨。
先上一个暴力:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#include<bits/stdc++.h> using namespace std; int n,r,q; struct per{ int s,w,id; }p[200003]; bool cmp(per a,per b){ if(a.s==b.s)return a.id<b.id; return a.s>b.s; } int main(){ cin>>n>>r>>q; for(int i=1;i<=(n<<1);i++){scanf("%d",&p[i].s);p[i].id=i;} for(int i=1;i<=(n<<1);i++)scanf("%d",&p[i].w); sort(p+1,p+1+(n<<1),cmp); while(r--){ for(int i=1;i<=(n<<1);i+=2){ if(p[i].w>p[i+1].w)p[i].s++; if(p[i].w<p[i+1].w)p[i+1].s++; } sort(p+1,p+1+(n<<1),cmp); } cout<<p[q].id; return 0; } |
STL受害者,用快排时间复杂度极高\(O(R(NlogN+N))\)
快排的快是针对随机数列来讲的(大部分情况下是这样),而这道题不同,每一轮过后,所有的胜利者的顺序不会变,所有的失败者的顺序也不会变,所以这个时候就要用归并排序了!!
归并排序和快排的区别(懒得打字了你们自己看图片吧)

归并排序
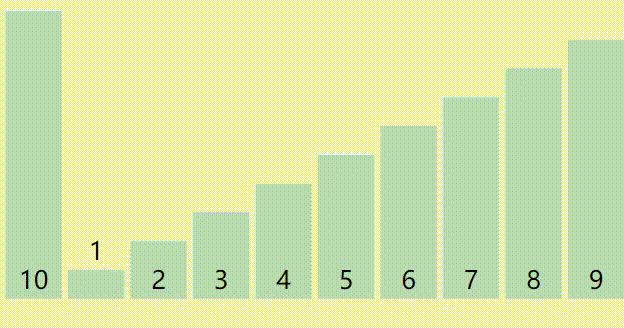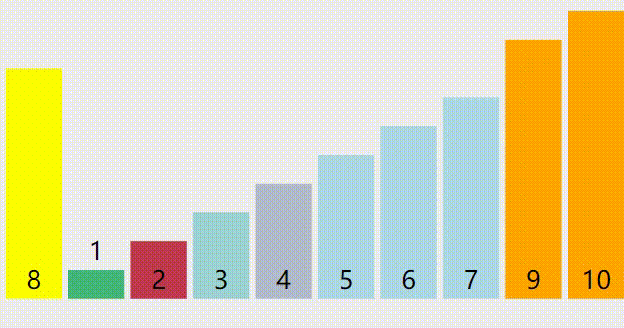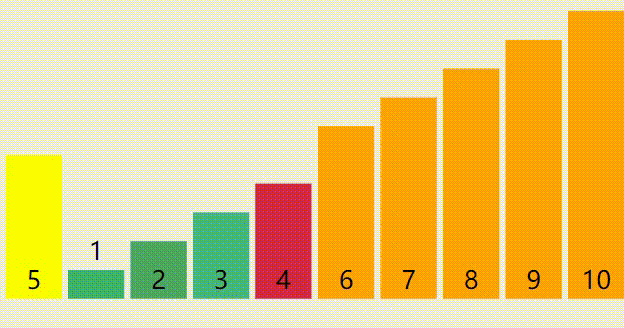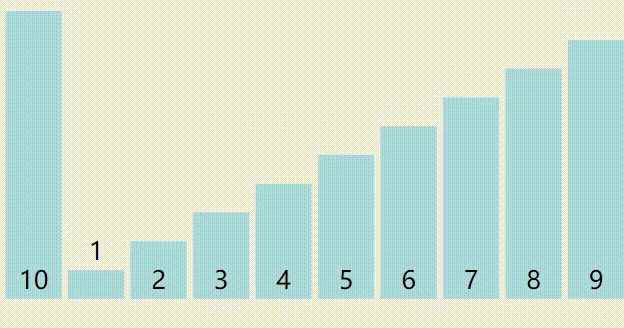
快排
看出来了吧,大家可以发现,归并排序每次的操作只针对相邻区间,或者说合并时是对相邻几个区间的操作,所以这符合只需要修改相邻几个分数的排布状况的题意。
然后就过了……
所以以后就算我用插入排序,用冒泡排序,我也不会用快排!!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
#include<bits/stdc++.h> using namespace std; const int MAXN=200003; int n,r,q; int id[MAXN],win[MAXN],lose[MAXN]; int s[MAXN],w[MAXN]; bool cmp(int a,int b){ if(s[a]==s[b])return a<b; return s[a]>s[b]; } void Merge(){ int i,j; i=j=1,id[0]=0; while(i<=win[0] && j<=lose[0]) if(cmp(win[i],lose[j])) id[++id[0]]=win[i++]; else id[++id[0]]=lose[j++]; while(i<=win[0])id[++id[0]]=win[i++]; while(j<=lose[0])id[++id[0]]=lose[j++]; } int main(){ cin>>n>>r>>q;n*=2; for(int i=1;i<=n;i++)id[i]=i; for(int i=1;i<=n;i++)scanf("%d",&s[i]); for(int i=1;i<=n;i++)scanf("%d",&w[i]); sort(id+1,id+1+n,cmp);//真香 while(r--){ win[0]=lose[0]=0; for(int i=1;i<=n;i+=2){ if(w[id[i]]>w[id[i+1]]){ s[id[i]]++; win[++win[0]]=id[i]; lose[++lose[0]]=id[i+1]; } else { s[id[i+1]]++; win[++win[0]]=id[i+1]; lose[++lose[0]]=id[i]; } } Merge(); } cout<<id[q]; return 0; } |
T5 传球游戏
其实这应该算是昨天的题目,在后面来一道水题
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
#include<bits/stdc++.h> using namespace std; int n,m,f[31][31]; int main(){ cin>>n>>m; memset(f,0,sizeof(f)); f[1][0]=1; for(int k=1;k<=m;k++){ f[1][k]=f[2][k-1]+f[n][k-1]; for(int i=2;i<=n;i++)f[i][k]=f[i-1][k-1]+f[i+1][k-1]; f[n][k]=f[n-1][k-1]+f[1][k-1]; } cout<<f[1][m]<<endl; return 0; } |