T1 求三角形的最大面积
题目大意:给你一个由多个三角形组成的大三角形,其中有些三角形缺失了,求出剩下部分最大的三角形。
毒瘤题,dp很好想,被特殊情况坑了。
首先上三角和下三角都要算一遍(其实就是反过来再找一遍)
就拿上三角来说,我们很容易就知道它的高度就是min(左,右)+1,但是实际上还要考虑一些特殊情况
比如下面这种情况:

输入的时候是这样的
|
1 2 3 4 5 6 |
3 #---# #-# # 0 |
所以在更新f[i][j]的时候要注意判断j的奇偶性就行了
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
#include<bits/stdc++.h> using namespace std; int n; int tri[300][300];//发现这东西是多余的 int f1[300][300],f2[300][300];//下三角和上三角 int main(){ while(233){ memset(tri,0,sizeof(0)); memset(f1,0,sizeof(f1)); memset(f2,0,sizeof(0)); scanf("%d",&n); if(n==0)break; for(int i=1;i<=n;i++){ char str[400]; scanf("%s",str+1);int len=strlen(str+1); for(int j=1;j<=len;j++){ tri[i][j+i-1]=(str[j]=='-'?1:0); f1[i][j+i-1]=f2[i][j+i-1]=tri[i][j+i-1];//可以放就初始化为1 } } for(int i=2;i<=n;i++){ int cnt=1; for(int j=i;j<=2*n-i;j++,cnt++){ if(f1[i][j]==0||cnt%2==0)continue;//偶数不能更新 f1[i][j]=f1[i][j]+min(f1[i-1][j+1],min(f1[i-1][j]==0?0:0x3f3f3f3f,f1[i-1][j-1]));//虽然讨论了左右的情况,但是中间不能为不能放的格子 } } for(int i=n-1;i>=1;i--){ for(int j=i;j<=2*n-i;j++){ if(f2[i][j]==0)continue; f2[i][j]=f2[i][j]+min(f2[i+1][j+1],min(f2[i+1][j],f2[i+1][j-1])); } } int ans=0; for(int i=1;i<=n;i++){ for(int j=i;j<=2*n-1;j++){ ans=max(ans,max(f1[i][j],f2[i][j])); } } cout<<ans*ans<<endl; } return 0; } |
T2 下楼问题
题目大意:有一个n层楼的建筑,现在有一只猫在楼顶,每层楼有三个门,现给出距离,求猫到1楼的最长距离(不能上楼也不走回头路)
由于每层楼之间是独立的,而且下了楼就不能往上,所以每层楼的状态具有无后效性,即我们不必关心当前状态是怎么来的。
我们考虑如何更新当前状态
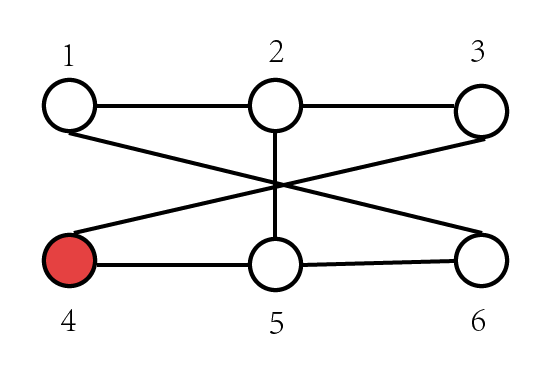
假设我们要更新4这个点,我们发现其余5个点都有到它的合法路径,如果我们用5更新4的话,会发现5状态也会需要4来更新,我更新我自己是不可以的。
于是我们可以只考虑上一层的来更新下一层的
先解释下变量吧,我觉得还是比较形象的
| 变量名 | 变量含义 |
|---|---|
| _path[i] | 第i层楼左边的路径长度 |
| path_[i] | 第i层楼右边的路径长度 |
| down[i] | 第i层楼中间门往下的路径长度 |
| down_[i] | 第i层楼左边门往右下的路径长度 |
| _down[i] | 第i层楼右边门往左下的路径长度 |
| f[i][j] | 走到第i层楼第j扇门的最长路 |
于是状态可以这样更新:
\(f[i][2]=max(f[i+1][2]+down[i+1],max(f[i+1][1]+down\_[i+1]+path\_[i],f[i+1][3]+\_down[i+1]+\_path[i]))\)
\(f[i][1]=max(f[i+1][3]+\_down[i+1],max(f[i+1][1]+down\_[i+1]+\_path[i]+path\_[i],f[i+1][2]+down[i+1]+\_path[i]))\)
\(f[i][3]=max(f[i+1][1]+down\_[i+1],max(f[i+1][3]+\_down[i+1]+\_path[i]+path\_[i],f[i+1][2]+down[i+1]+path\_[i]))\)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
#include<bits/stdc++.h> using namespace std; const int MAXN=500003; int f[MAXN][4];//1-left 2-middle 3-right int _path[MAXN],path_[MAXN]; int down[MAXN],down_[MAXN],_down[MAXN]; int n; int main(){ // freopen("test.out","w",stdout); int t,T;scanf("%d",&t);T=t; while(t--){ scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d%d%d%d%d",&_path[i],&path_[i],&down_[i],&down[i],&_down[i]); } f[n][2]=_path[n];f[n][1]=0;f[n][3]=path_[n]+_path[n]; for(int i=n-1;i>=1;i--){ f[i][2]=max(f[i+1][2]+down[i+1],max(f[i+1][1]+down_[i+1]+path_[i],f[i+1][3]+_down[i+1]+_path[i])); f[i][1]=max(f[i+1][3]+_down[i+1],max(f[i+1][1]+down_[i+1]+_path[i]+path_[i],f[i+1][2]+down[i+1]+_path[i])); f[i][3]=max(f[i+1][1]+down_[i+1],max(f[i+1][3]+_down[i+1]+_path[i]+path_[i],f[i+1][2]+down[i+1]+path_[i])); } int ans=max(f[1][1],max(f[1][3],f[1][2])); printf("Case %d: ",T-t); cout<<ans<<endl; } return 0; } |
T3 瞬移
题目大意:有两个人在一个0-1矩阵上进行移动,其中是不可走的位置。他们每次只能从当前行移动到下一行,而且两个人的位置x,y必须满足限制:\(x+m_i\le y\le x+m_a\) . 一个人移动到下一行的代价为其横坐标变化值的绝对值。问两个人都到达底端需要的最小消耗.
做惯了大数据的题目,做一些比较小的数据的题目都不敢大胆去想了,这题目n只有1000而m只有10,对于师傅和徒弟两个人,我们可以五重循环分别枚举层数 当前徒弟位置 当前师傅位置 上一层徒弟位置 上一层师傅位置 这样的时间复杂度达到了惊人的\(O(NM^4)\)然而由于数据范围较小,所以并不会超时.
我们可以用f[dep][i][j]表示dep层师傅在i徒弟在j时所需要耗费的最小值,枚举上一层的状态即可更新.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
#include<bits/stdc++.h> using namespace std; int n,m,l,r,x,y; int ma[1003][12]; int f[1003][13][13]; int main(){ int t;scanf("%d",&t); while(t--){ memset(f,0x3f,sizeof(f)); scanf("%d%d%d%d%d%d",&n,&m,&l,&r,&x,&y); x++,y++; for(int i=1;i<=n;i++){ char tmp[20]; scanf("%s",tmp+1); for(int j=1;j<=m;j++)if(tmp[j]=='*')ma[i][j]=1;else ma[i][j]=0; } for(int i=1;i<=m;i++)ma[1][i]=0;//第一层就把师傅徒弟的初始位置标记为合法,其他为不合法 ma[1][x]=ma[1][y]=1; f[1][x][y]=0; for(int dep=2;dep<=n;dep++){//层数 for(int j=2;j<=m;j++){//徒弟 if(!ma[dep][j])continue; for(int i=1;i<j;i++){//师傅 if((!ma[dep][i])||j<i+l||j>i+r)continue; for(int k=2;k<=m;k++){//上层徒弟 if(!ma[dep-1][k])continue; for(int z=1;z<k;z++){//上层师傅 if((!ma[dep-1][z])||k<z+l||k>z+r)continue; f[dep][i][j]=min(f[dep][i][j],f[dep-1][z][k]+abs(z-i)+abs(k-j)); } } } } } int mi=1<<30; for(int i=2;i<=m;i++){ if(!ma[n][i])continue; for(int j=1;j<i;j++){ if((!ma[n][j])||i<j+l||i>j+r)continue; mi=min(mi,f[n][j][i]); } } cout<<mi<<endl; } return 0; } |
T4 数字游戏
题目大意:给你n个数,每个数有一个衰减值,m个回合,每个回合你可以选一个数(选完消失并计入答案),选完后剩余的数衰减。求能选到的最大的总和是多少。
可以比较容易地发现一个结论:如果n=m,就是所有数都会被选到的话,要根据bi的大小来选,先去掉那些每回合损耗多的,再去掉损耗少的,这样显然就是最优的。
但如果m<n呢?设想:假如己经选定了m个数,只去掉这m个数,那么与m=n的情况一样,我们一定是按照bi的大小来去掉的。因为显然对于选定的个数,这样做最优。
到这里,我们就会想到采用动态规划的方法。把n个数按照bi从大到小排序,然后问题就转化为对于一个n个数的序列,从中选择m个数,第i个选择的数权值为A-B*i,(A,B分别为此数在原来a,b数组里对应的值),使得所有权值的和最大。
不难写出下面的动态规划状态转移方程:
f(i,j)=max(f(k,j-1)+a_i-b_i \times(j-1)
f(0,0)=0
其中,1\le i\le n ,1\le j\le m,0\le k<j,ai,bi为排序后第i个数相应的值。这样的复杂度是O(n^3)
再进一步分析,很容易地把上述动态規划方程改变为下面的形式:
令F(i,j)前i个数当中取了j个数的最优解,则
F(i,j)=max(F(i-1,j),F(i-1,j-1)+a_i-b_i\times(j-1)
F(0,0)=0
这样,时间复杂度就降到了O(n^2)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
#include<bits/stdc++.h> using namespace std; int n,m; struct node{ int a,b; }num[203]; int f[203][203]; bool cmp(node a,node b){ return a.b>b.b; } int main(){ cin>>n>>m; for(int i=1;i<=n;i++)scanf("%d",&num[i].a); for(int i=1;i<=n;i++)scanf("%d",&num[i].b); sort(num+1,num+1+n,cmp); for(int i=1;i<=n;i++){ for(int j=1;j<=m;j++){ f[i][j]=max(f[i][j],max(f[i-1][j],f[i-1][j-1]+num[i].a-num[i].b*(j-1))); } } cout<<f[n][m]<<endl; return 0; } |
写得好写得好
留坑不填,禁赛一年。